5 Essential Self-Balancing Trees You Must Know: AVL, Red-Black, Splay & More

Introduction
Self-balancing trees are an essential category of binary search trees (BSTs) that automatically maintain their balance to ensure optimal time complexity for insertion, deletion, and searching operations. Unlike unbalanced BSTs, which can degrade to linear time complexity in the worst case, self-balancing trees maintain logarithmic height (O(log n)), making them highly efficient for large datasets.
This guide explores five fundamental types of self-balancing trees: 5 Essential Self-Balancing Trees You Must Know: AVL, Red-Black, Splay & More. We will cover their structures, balancing techniques, and real-world applications.
Importance of Balanced Trees in Computing
Maintaining a balanced tree structure improves computational efficiency in various domains, including:
- Database Indexing: Speeds up queries and retrieval operations.
- File Systems: Enhances file search and directory traversal.
- Network Routing: Optimizes routing tables for quick lookups.
- Gaming Engines: Ensures real-time leaderboard updates and object tracking.
- AI & Machine Learning: Improves the efficiency of decision trees.
1. AVL Trees: Strict Balancing for Faster Searches
1.1 What is an AVL Tree?
The AVL Tree (named after Adelson-Velsky and Landis) was the first self-balancing BST. It maintains a balance factor for each node, defined as the height difference between the left and right subtrees:
Balance Factor=Height of Left Subtree −
Height of Right Subtree
An AVL tree ensures that this balance factor is always -1, 0, or 1, keeping the tree strictly balanced.
1.2 Rotations and Balancing Mechanism
If an operation causes an imbalance, AVL trees use rotations to restore balance. These include:
- Right Rotation (Single Rotation – RR): Used for left-heavy trees.
- Left Rotation (Single Rotation – LL): Applied to right-heavy trees.
- Left-Right Rotation (Double Rotation – LR): A combination of left and right rotations.
- Right-Left Rotation (Double Rotation – RL): A combination of right and left rotations.
To Understand in the Deep Visit the Visual Algo How it Works : https://www.cs.usfca.edu/
~galles/visualization/AVLtree.html
1.3 Applications and Use Cases
- Database Indexing: Keeps query response times low.
- Memory Allocation: Used in heap memory management.
- File Systems: Ensures efficient directory organization.
1.4 Advantages and Limitations
✅ Pros: Faster search times due to strict balancing.
❌ Cons: More rotations required, leading to higher maintenance costs.
To Understand and More Deep About AVL Trees Visit : https://medium.com/basecs/the-little-avl-tree-that-could-86a3cae410c7
2. Red-Black Trees: Faster Insertion and Deletion
2.1 What is a Red-Black Tree?
A Red-Black Tree is a balanced BST where each node follows the following rules:
- Each node is either Red or Black.
- The root node is always Black.
- Red nodes cannot have red children (no two consecutive red nodes).
- Every path from root to a leaf has the same number of Black nodes.
These properties ensure a balanced structure with minimal rotations.
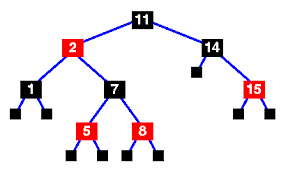
2.2 Balancing Mechanism
Red-Black trees balance using:
- Recoloring: Adjusting node colors to maintain properties.
- Rotations: Similar to AVL tree rotations (LL, RR, LR, RL).
To Understand in the Deep Visit the Visual Algo How it Works : https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
2.3 Real-World Applications
- Linux Kernel: Used in process scheduling.
- Java’s TreeMap & C++ STL Map: Ensures O(log n) operations.
- Networking: Efficient routing table management.
2.4 Advantages and Limitations
✅ Pros: Faster insertions and deletions than AVL Trees.
❌ Cons: Searching can be slightly slower compared to AVL due to relaxed balancing.
To Understand and More Deep About Red-Black Trees Visit : https://medium.com/basecs/painting-nodes-black-with-red-black-trees-60eacb2be9a5
The Technical Difference Between the AVL Tree and Red-Black Tree : https://stackoverflow.com/questions/13852870/red-black-tree-over-avl-tree
3. Splay Trees: Self-Adjusting Efficiency
3.1 What is a Splay Tree?
A Splay Tree is a self-adjusting BST that moves recently accessed nodes to the root. This makes frequently accessed nodes available in O(1) time after an initial O(log n) search.
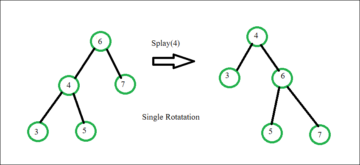
3.2 Splaying Mechanism
Operations in a splay tree involve rotations, known as splaying:
- Zig: Single rotation when the node is a child of the root.
- Zig-Zig: Double rotation when the node and parent are in the same direction.
- Zig-Zag: Double rotation when the node and parent are in opposite directions.
To Understand in the Deep Visit the Visual Algo How it Works : https://www.cs.usfca.edu/~galles/visualization/SplayTree.html
3.3 Applications
- Web Caches: Optimizes page retrieval.
- Memory Management: Enhances garbage collection performance.
- Data Compression: Improves Huffman coding efficiency.
3.4 Pros and Cons
✅ Pros: Faster for frequently accessed elements.
❌ Cons: Worst-case time complexity is O(n) for unbalanced access patterns.
To Understand and More Deep About Splay Trees Visit : https://www.geeksforgeeks.org/introduction-to-splay-tree-data-structure/
4. Treaps: Randomized Balancing with Priority Values
4.1 What is a Treap?
A Treap combines a Binary Search Tree (BST) and a Heap. Each node contains:
- A key (maintains BST order).
- A priority (maintains heap order).
The tree is balanced probabilistically based on priority values.
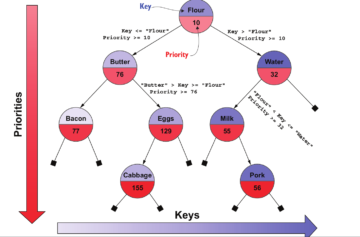
4.2 Balancing Strategy
During insertion and deletion, the tree rotates nodes based on priority to maintain heap properties.
4.3 Applications
- Load Balancing: Distributes workloads evenly.
- Network Routing: Helps optimize network path selection.
- Randomized Algorithms: Used in dynamic graph algorithms.
4.4 Pros and Cons
✅ Pros: Simple implementation, randomized balancing.
❌ Cons: No strict balance guarantees.
5. B-Trees: The Backbone of Database Indexing
5.1 What is a B-Tree?
A B-Tree is a self-balancing tree optimized for disk storage and databases. Unlike BSTs, B-Trees:
- Have multiple keys in a single node.
- Use order M, meaning each node has at most M children.
- Balance by redistributing keys among nodes.
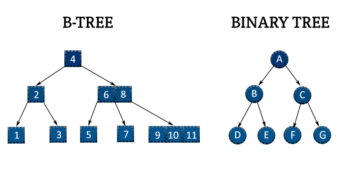
5.2 How B-Trees Work
- Insertion: Keys are added, splitting nodes when necessary.
- Deletion: Keys are removed, merging nodes if required.
To Understand in the Deep Visit the Visual Algo How it Works : https://www.cs.usfca.edu/~galles/visualization/BTree.html
5.3 Applications
- Databases (MySQL, PostgreSQL, MongoDB): Used for indexing.
- File Systems (NTFS, HFS+): Organizes files for fast access.
- Search Engines (Google, Bing): Optimizes search query retrieval.
5.4 Pros and Cons
✅ Pros: Optimized for disk access, efficient indexing.
❌ Cons: More complex than other self-balancing trees.
6. Comparative Analysis of Self-Balancing Trees
| Tree Type | Insert/Delete | Search | Best Use Case |
|---|---|---|---|
| AVL | O(log n) | O(log n) | Read-heavy applications |
| Red-Black | O(log n) | O(log n) | General-purpose usage |
| Splay | O(log n) | Amortized O(1) | Frequently accessed data |
| Treap | O(log n) | O(log n) | Randomized balancing |
| B-Tree | O(log n) | O(log n) | Database indexing |
Conclusion
Self-balancing trees play a crucial role in maintaining efficient operations in databases, operating systems, and computer networks. Each tree type has its strengths, and choosing the right one depends on the specific application requirements.
Understanding these structures ensures better implementation decisions for software engineers and computer scientists.











